excel 怎么算矩阵

Excel 中的矩阵运算技巧详解

在Excel中,矩阵运算是一种非常强大的工具，它能够帮助用户进行数据处理、数据分析和建模等任务，本文将详细介绍如何使用Excel来进行各种矩阵运算，并附有详细的步骤说明和例子。

理解基本概念

在开始之前,首先需要理解一些基本的概念：

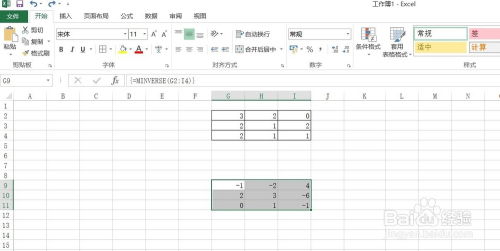
• 行列式：行列式是矩阵的一个重要特性，用于衡量矩阵的大小。
• 转置矩阵：通过交换矩阵中的行与列来创建一个新的矩阵。
• 逆矩阵：对于可逆矩阵，其逆矩阵可以用来求解线性方程组或进行矩阵变换。

创建矩阵

在Excel中,可以通过以下几种方式创建矩阵：

直接输入法

1. 打开Excel并进入一个工作表。
2. 在单元格A1到D3中分别输入数字,形成一个3x4的矩阵（2 4 6；7 9 11；13 15 17）。
3. 按下Enter键完成每行数据的输入。

填充序列

1. 在A1单元格输入数字1,然后向下拖动填充柄至E1以创建一系列连续的数字。
2. 选择B1:C1，右击并选择“插入”>“复制”，再选D1:E1，右击并选择“粘贴特殊”>“序列”>“序列类型：行”>输入公式=ROW(A1)。
3. 这样生成了从1到8的一系列连续整数。

计算矩阵元素

基本运算

• 加减乘除：直接在单元格中相加、相减、相乘、相除。
• 矩阵加减：对对应位置的元素进行加减操作。
• 矩阵乘法：
  • 对于两个矩阵A和B,如果A为m×n的矩阵，B为n×p的矩阵，则结果C将是m×p的矩阵。
  • Cij = Σk=1^n Aik * Bkj (其中i是行索引，j是列索引)

特殊函数

• MUL：快速计算矩阵的乘积。
• SUM：求矩阵的元素总和。
• MIN 和 MAX：分别求矩阵的最小值和最大值。

转置矩阵

转置矩阵是一个简单的操作：

• 将原矩阵的行转换成列,即每个元素的位置颠倒。

给定矩阵

1 2 3
4 5 6
7 8 9

其转置后为

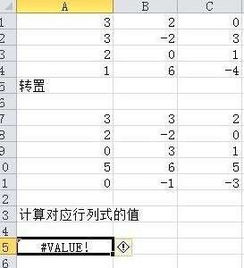
1 4 7
2 5 8
3 6 9

逆矩阵

找到一个矩阵的逆矩阵需要满足以下几个条件：

• 可逆矩阵的行列式的绝对值不等于0。
• 存在一个唯一的矩阵X使得AX = I，其中I是单位矩阵。

在Excel中,通常无法直接计算逆矩阵，但可以通过MATLAB或Python脚本结合Excel进行计算。

Excel作为一款功能强大的电子表格软件,提供了丰富的工具和函数来处理矩阵运算，通过上述介绍，希望你能够掌握这些基本操作，并能根据具体需求灵活应用，在实际工作中遇到复杂的问题时，可能还需要借助专业的数学软件或编程语言来实现更高级的功能。